Solve your most complex pricing challenges with next-generation software from the pioneers of Revenue Management.
Solve your most complex pricing challenges with next-generation software from the pioneers of Revenue Management.
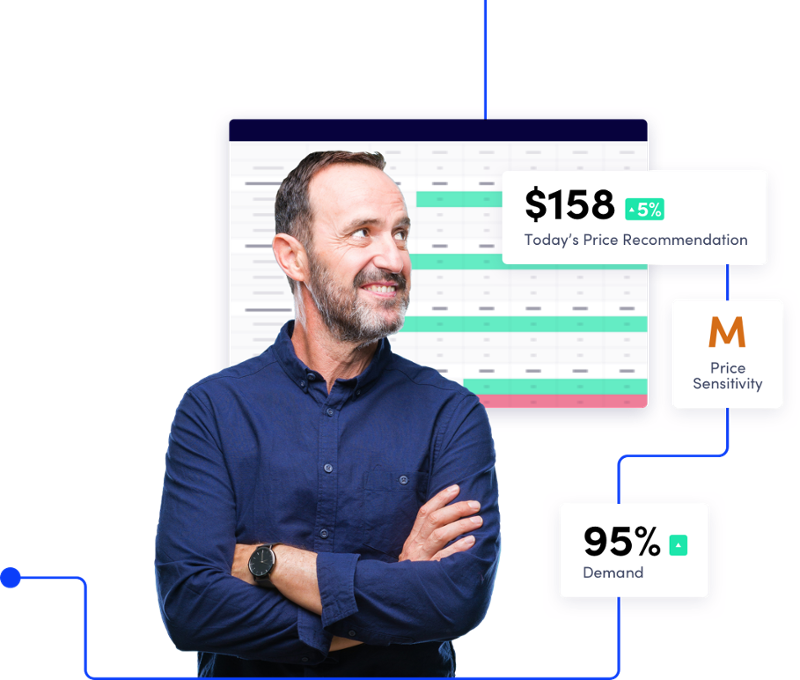















“It gives us the confidence and data to stand behind tough decisions. No conventional wisdom would have told me to raise my rates on those dates.”
Head of Revenue Management
Midmarket Hotel Group

“This totally changed the game for us. Profits are up, price exceptions are way down, and the sales force is completely bought into the price guidance.”
SVP of Pricing
Paper & Packaging Leader

“As the marketplace evolves, better analytics tools will be required by our sellers. Revenue Analytics is the partner that will enable these capabilities.”
Al Lustgarten, SVP, Technology and Information Services
Hearst


“This new technology will help us provide even more reasons for our customers to book and travel with us.”
Commercial Director
Leading Passenger Rail Operator
Many brands are looking for better RM solutions to help them survive the months ahead and thrive in the years to come. We can help. Speak to an expert today.


